To estimate tank water usage and overflow frequency, the R function tankmodel.R is used. This function requires input of the following variables (some of which EBI calculator requires the user to enter, and others that EBI calculator assumes values for).

1. Daily runoff or rainfall data. EBI calculator uses daily runoff data for Croydon over three years that were chosen from the available record (6 minute records) from that site for which there was no missing data, and no accumulated data > 1 day in duration. The three years chosen represent a year with average rainfall (1965 &ndash actually 1 Apr 1965 &ndash 31 Mar 1966, with 950 mm of rain), a dry year (1967 with 660 mm), and a wet year (1970, with 1085 mm). Runoff was derived from hourly data (while none of the chose years had missing data, 1967 and 1970 each had nine blocks for which rainfall was aggregated, ranging from 2 to 24 hours &ndash for all but 3 of these blocks, the aggregated data was distributed across the blocks in proportion to rain that was recorded at the Melbourne station over the same block. For the remaining 3 blocks for which Melbourne also lacked data (all < 8 h), the aggregated rainfall was distributed evenly across the block. Runoff was estimated from the hourly data by assuming that the first 1 mm in a rain event was lost to evaporation (and therefore did not become runoff), and that a rain event was defined as any record of rain that followed at least one hour of zero recorded rain. This calculation of hourly runoff for the Croydon record was calculated using the function compile.inflow.R, and then converted to daily runoff.
2. Tank volume, and the volume of water in the tank at the beginning of the simulation. EBI calculator uses the value entered for tank volume in the second tab, and assumes that the tank was 50% full at the start of the simulation (although the script contains 'commented-out lines that allow for a 'burn-in' run of the model before simulation, which is not used).
3. Catchment area for the tank. EBI calculator uses the roof area values and percentage draining to roof values entered in the first tab for this variable.
4. Initial loss of rainfall before it becomes runoff. EBI calculator sets this to zero, because initial loss has been estimated already in the runoff input vector.
5. First flush volume. EBI calculator requires this as an input. There are many types of first flush diverters that divert varying amounts of water from the tank before allowing runoff to enter. A critical assumption for EBI calculator is that any diverted first flush water either overflows to the modelled raingarden, or if there is no raingarden to the property's normal garden. If first flush water is diverted to a stormwater drain, then the estimated benefit to the stream should be considered zero.
6. Number of people living in the house. EBI calculator uses the number of people entered in the first tab. This is used to calculate consumption patterns as below.

Water usage volumes are assumed as follows after Wilkenfield and associates (2006. Water saving requirements for new residential buildings in Victoria: options for flexible compliance. Melbourne: Department of Sustainability and Environment.). When each use is selected on the second tab the following values are used.

7. Toilet. EBI calculator assumes toilets use 18.9 L per person per day.
8. Washing machine. EBI calculator assumes washing machines use 35.31 L per day for the first person and 23.54 L for each additional person.
9. Hot water systems. EBI calculator assumes that hot water systems use 46.9 L per person per day (calculated from Wilkenfield's estimate of 61.9 minus half the washing machine use).
10. Garden area. EBI calculator uses the value entered in the second tab
11. Annual outdoor irrigation and monthly distribution. EBI calculator assumes garden watering uses 12,971 L per 100 m² of garden per year, spread over the 12 months of the year in the following proportions: 0.27, 0.21, 0.09, 0.07, 0.05, 0, 0, 0, 0.03, 0.04, 0.04, 0.2.
12. Other uses. The function (in the R function, but not given as an option on the web calculator) allows the user to supply their own monthly usage patterns which are then spread evenly across the days of each month. EBI calculator assumes zero other uses, but allows them to be entered in the second tab.
13. Use for drinking and car-washing has very small effects on yield, and have not been included as options. They could be included as part of other uses.

EBI calculator takes uses selected and the number of people and calculates and estimated daily demand for the house for water from the tank, over the 3 years. (The program actually uses a matrix of demand patterns for all possible combinations of uses for the given number of people and the given garden area.) For each day over the period, inflow from runoff is added to the volume in the tank at the end of the previous day and subtracts the demand that can be extracted from the available volume. If the demand exceeds the volume in the tank at the start of the day, then only the available volume is used. If the inflow exceeds the space available in the tank after demand is extracted, then the excess is assumed to overflow from the tank.

tankmodel.r records the complete time series of water consumed, that overflowed and that remained in the tank each day, and from these records calculates three indices (stream, nitrogen and water), and their average, the EBI (averaged over the full three-year period).

The stream index is a measure of the reduction in runoff frequency afforded by the tank. It is assumed that runoff is generated from the roof 121 days per year, and that overland flow would have been generated from the pre-urban forest floor 12 days per year. Furthermore, it is assumed that any impervious areas that are not connected to the formal (piped) stormwater drainage system do not contribute to increased runoff frequency (while this is unlikely to be the case, the finding that such areas currently have no detectable environmental impact compared to the directly connected impervious areas, they are not considered a high priority for treatment). The stream index is calculated as:

,

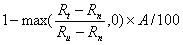where A = the area (m²) of currently connected roof to be drained by the tank; R_t = number of days of runoff per year from A following treatment; R_n = frequency of runoff from A in pre-urban state (15 days per year0; R_u = frequency of runoff from A before treatment (121 days per year). All three indices are standardized by impervious catchment area: one unit measures the environmental benefit from 100m².

The water index is the proportion of the total harvestable yield from A that is collected and used by the rainwater tank, multiplied by A/100.

The nitrogen index is 1 minus the ratio of nitrogen load overflowing from the tank to the nitrogen load running off that part of the tanks catchment area that is currently connected to the stormwater system. It is assumed that there is no loss of nitrogen in the tank, that all overflowing water from the tank has the same nitrogen concentration as the water flowing in, and that all consumed water keeps water from the creek. (Irrigation water nitrogen is assumed to be taken up by plants, and nitrogen water used in household appliances is assumed to be exported from the catchment. This nitrogen is likely to end up in the sewage treatment plant, and because the nitrogen is replacing mains water nitrogen, it is assumed to have no net effect). However, for properties with septic tanks (identified in the first tab), it is assumed that any water that is used in household appliances will drain to the creek, as septic tanks are efficient nitrifyers and nitrate will efficiently drain through soils to the creek. Thus for properties with septic tanks only the nitrogen load in water used for garden watering is used to calculate the nitrogen index.

The overall Environmental Benefit Index (EBI) is the weighted average of the three sub-indices:
0.5*Stream index + 0.3*Nitrogen index + 0.2*water-saving index
for runoff from roofs and 0.625*Stream index + 0.375* Nitrogen index
for runoff from paved areas

EBI calculator allows the modelling of four simple scenarios:
a) a tank by itself,
b) a rain-garden by itself
c) a tank and a rain-garden with no interaction (note in this case, an unchecked assumption is that diverted first flush water from the tank goes to the garden and not the stormwater drain), and
d) a tank whose overflow (and first flush) drains to the raingarden.

More complex scenarios can be modelled by using the R-functions outside the webpage environment, or by running EBI calculator in separate runs and doing some simple calculations. For instance, to estimate the EBI improvement of connecting an existing rainwater tank to household appliances, first calculate EBI scores for the existing set up, and then calculate the scores for the proposed set up. The EBI improvement that could attract a rebate is the difference between the two.

Raingarden behaviour is modelled using the function gardenmodel.R. This function requires the following variables:
#data.frame with hourly inflow vol in L and
#first three columns datetime, date, year, month
#all class chron (compiled #using function compile.inflow()) and one column of inflow data
hrunoff, #as for compile inflow - only used to calculate urban N load
et,
#vector the same length as inflow$datetime with
#matching evapotranspiration values in mm/h
Af, Pf, Hf, #filter area (sq m) perimeter (m) and depth (m)
Ap, Hp, #pond area (sq m) and depth (m)
isveg = TRUE, # logical, TRUE if the raingarden has at least 50% recommended vegetation cover
lined.bottom = TRUE, # logical Ksu = 0 if TRUE, 0.0005 if FALSE (dm/h)
lined.side = TRUE, # logical - can only be true if lined.bottom is TRUE
medium = "loamy sand", #filter medium, must be sandy loam, sand, or gravel (scoria)
#decides Ksf = 1,2.5, 36 (dm/h) respectively (assumes 50% reduction in
#Ks for loamy sand and sand over time)
Ho, #distance from base to invert of outlet pipe (m)
#if no outlet pipe set Ho to Hf + Hp
Vstart, # Vol of water in system at t1 in L (EBcalc assumes filter is half full at start)
carea, carea.tank, # impervious area draining directly to tank, and catchment area of any tank
# that might overflow into the garden
prop.pave = 1#proportion of carea that is paving (as opposed to roof)

It uses hourly timestep rainfall data as its primary inflow for runoff from impervious surfaces that directly flow into the rain-garden. If the rain-garden is to also receive first-flush flows or overflow from a tank, then EB calculator converts the daily flow outputs from the tank model, by taking the daily first-flush volumes and distributing them in the first hourly rain records of the appropriate day, and similarly distributing daily overflow volumes to the last hourly rain records of the day.

For each hour, the water volume in the filter is distributed among exfiltration to underlying soil (if unlined: if the sides are unlined then exfiltration is also assumed from the walls of the filter), flow out of the outflow pipe in the filter (if present), evapotranspiration (if vegetated), and overflow (if the rain-garden fills).

Any overflow volume in a day is counted as runoff, as is any flow from the outflow pipe greater than the acceptable hourly volume. The acceptable hourly flow equals the depth of flow observed in a reference creek (Olinda Creek at Mt evelyn) at the peak of an event that is sufficient to commence overland flow: about 6 m³/s for a 31.8 km² catchment = 0.068 mm/h.

Any overflow water from the rain-garden is assumed to have no reduction in nitrogen concentration, and any water filtering into the underlying soil is assumed to have complete loss of nitrogen. Water flowing out of the outlet pipe in the filter is assumed to have different degrees of nitrogen loss (or gain) depending on the medium type and whether the rain-garden is vegetated, and for loamy sand, antecedent dry-weather period. The following table summarises the rules used.

Medium	Vegetation type	Normal (wet)	After Dry
Loamy sand	Veg	59%	If ADWP <=4 days then Removal = 59% Else Removal = 59% - 0.3% x ADWP (days)
	Unveg	-101%	If ADWP <=5 days then Removal = -101% Else Removal =-101% - 0.2% x ADWP (days)
Sand	Veg	72%	72%
	Unveg	32%	32%
Gravel (Scoria)	Unveg	39%	39%

Note the calculator does not allow the option of a vegetated gravel rain-garden.